隧道开挖对地下水扰动影响与区域水运移规律分析

1 工程概况

本工程位于邢台市，多数地区为中低山区，地势西高东低、北高南低。区域内山峰群立，层峦叠嶂，最高山峰为天河梁，海拔1 753 m，最低点位于石店村前河滩，海拔62 m。

研究对象路罗隧道、前营隧道等隧道洞口导洞海拔在900~1 100 m，邢台大峡谷景区各景点海拔在700~900m，景区下游各村庄海拔在500~700 m。隧道位于太行山主脉东侧，受构造强烈切割影响，峡谷走向基本以西北东南向为主，山体地层复杂，区内地下水主要以第四系孔隙潜水、基岩裂隙水为主。

由于岩层节理裂隙较发育且线路高程相对较低，隧址区段隧道洞身从王山铺村以东约800 m的峡谷地下穿过，王山铺村村民饮水均取半山腰处流出的构造裂隙水，为隧道穿越的沟谷中流水的上游。而沟谷水流向贺坪峡风景区，风景区位于沟谷的下游。为研究隧道施工对村民取水和风景区水源的影响，结合无人机航拍地形图开展地表水径流分析，并基于地形三维建模研究隧道开挖对下游地下水的影响深度。

2 航测方案

采用B厂家无人机对王山铺、周公山景区入口、邢台大峡谷景区、邢台大峡谷以及前营隧道平导口5处进行重点区域精飞，采用GPS坐标系CGS2000_ALBERS，航向重叠率为85 %，旁向重叠率为80 %，相机倾斜角42°，飞行速度3 m/s，航拍过程中会采集区域内的图像资料以及地形点云信息。在此基础上，采用A厂家无人机对上游山西省一部分区域以及大峡谷下游到路罗站入口的区域开展全局点云信息采集，覆盖隧址区上下游水系，测绘范围覆盖面积为52.24 km²。

结合A厂家和B厂家的无人机地形图测绘资料，将航飞工作区域内的航测数据整合拼接出带有三维坐标信息的地形图，再将无人机采集的点云地形信息导入Rhinoceros 7中，生成三维地形，发现隧址区内业有3条主干河道，分别位于前营隧道平道口处、邢台大峡谷流域以及周公山下游。路罗隧道正好横穿了三大主干河道所在的流域，因此，本研究重点针对隧址区内三大河道所在流域展开地下水运移模拟。

3 研究区汇水模型与分析

对研究区域进行汇水分析。汇水方向的确定通常采用D8（Deterministic Eigh thours）算法进行计算，假定被处理栅格内的水只流向其周围各栅格中的一个，并指向坡降最大的方向。将目标栅格同相邻各栅格进行比较，目标栅格中心与相邻栅格中坡降最大栅格中心的连线方向为目标栅格的水流方向。用128、1、2、4、8、16、32、64这8个特征码表示东北、东、东南、南、西南、西、西北和北8个有效的水流方向。

逆向跟踪汇水方向，统计注入该栅格的周围栅格数量，作为该栅格的汇流特征值。汇流特征值数值越大，表明注入的水流就越多。规定集水区为集水能力强栅格所在的区域，若某区域集水能力特征值为零，则代表该区域地势较高，据此可划分出研究区域分水岭的空间分布和集水区的边界。将栅格集水量为0的区域作为集水区分界线，进而划分区流域范围。图1将流域分为5个级别，但可以清晰发现，根据流域的划分同样可以将隧址区划分为3个主要的流域，划分结果和河网分布的分析结果一致。利用GIS软件将数据库中数据写入MODFLOW格式文件中。其中降雨入渗输入Recharge程序包，对应数据存入“*.rch”文件中；边界侧向补给量、开采量输入到Well程序包，对应数据存入“*.wel”文件。

图1 河网流域分布地形

为探究各水域水量汇集分布占比，需要对河网各级河道的倾泻点进行识别，具体原理即从每条河流的最高点出发，沿着坡降线往下，找到与其他支流汇集的交界处，对交界处进行标注。

图2（a）识别出了各级别河道的倾泻点，基于倾泻点，可计算出隧址区内所有河道汇集到各个倾泻点的流量大小，进而计算出地表水流量的分布及各流域的流量占比。如图2（b）所示，根据倾泻点流量统计，可将图1的3大主要流域细化分为20个级别的小流域，根据图中信息可知，图2（a）中颜色较深的流量大，流量单元最高达到了6 964，颜色靠较浅的流量越小，流量单元最低为1。

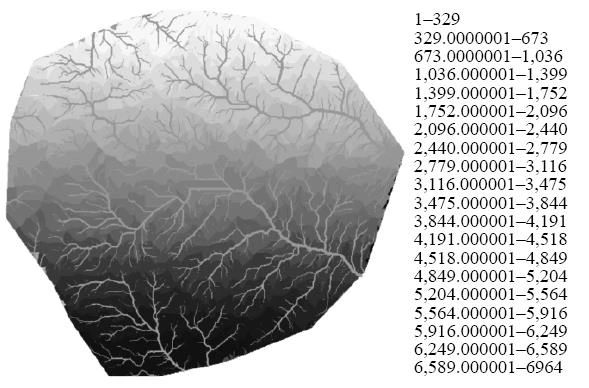
（a）

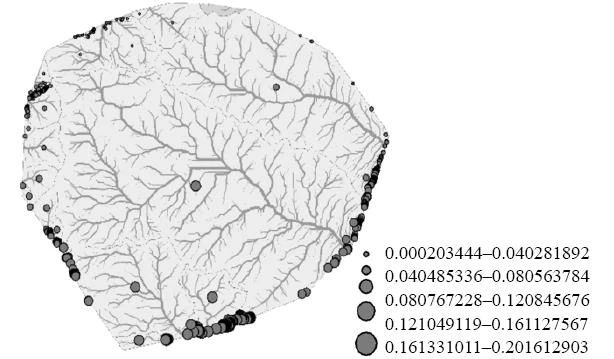
（b）

图2 流量分布地形及流量比例分布地形

（a）示意一;(b)示意二

利用盆域分析计算可知，在三大流域中，位于前营隧道平导口附近的流域流量最大，邢台大峡谷流域流量次之，最后是周公山流域一带。根据图2（b）中小球所示比例，计算得出前营隧道平导口流域集水占比为49.99 %，邢台大峡谷流域占比为33.31 %，周公山流域占比为16.70 %。考虑隧址区面积占比，前营隧道平导口流域面积占隧址区24.93 %，邢台大峡谷流域面积占隧址区53.36 %，周公山流域面积占比为21.71 %。

计算得到前营隧道平导口的集水比为2.005，邢台大峡谷流域的集水比为0.624，周公山流域的集水比为0.769。因此，考虑地表水的汇集能力，前营隧道平导口流域大于周公山流域大于邢台大峡谷流域，具体见表1。

表1 隧址区流量比、面积比、集水比

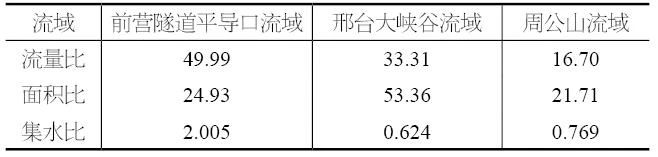
汇水分析结果显示，本区域内地表水系发育丰富，水系几乎笼罩整个区域，但是多为低流量支流，主干河道只要有3条，形成了本区域的三大流域，分别是前营隧道平导口流域、邢台大峡谷流域以及周公山一带流域。三大流域集水能力从大到小分别是前营隧道平导口流域大于周公山流域大于邢台大峡谷流域。

4 三维网络模型与渗流模拟数值

4.1 渗透试验

设备系统为刚性伺服岩石力学试验机，可以进行岩石力学单轴压缩试验，岩石力学三轴压缩试验，岩石力学渗流试验，以及岩石力学高温加载试验（最高温度可达200℃）。最大轴向压力200 t，最大围压可达到70 MPa，最大孔隙水压可达70 MPa，水压测量误差不大于±2 %，水压分辨率1 kPa，水流量不大于±2 %。变形测量为LVDT测量方式，轴向0~5 mm，径向0~2 mm，分辨率0.000 1 mm，测量误差不大于±1 %。

本研究采用稳态法测量，即保持一定水压与围压，监测水流量–时间关系曲线，水流量在该水压与围压条件下保持稳定均匀流速，根据达西定律测算渗透系数，此时流量–时间关系曲线为斜直线，其斜率为单位流量。

根据达西公式：流体流量与岩石的横截面积A、进出口端压差成正比；与岩样长度L、流体容重成反比。

4.2 渗流场计算

根据无人机获得的三维高程信息生成三维等高线，采用Rhinoceros7构建三维几何模型，并采用网格剖分软件griddle生成数值计算模型。计算模型采用实体单元，共划分848 362个四面体单元和159 885个节点；模型尺寸为：长×宽=5 300 m×5 300 m。

采用FLAC 3D单渗流模块建立数值模型，计算初始应力状态，并对位移场和塑性区进行清零，提出初始应力场对后续开挖的影响，当不平衡比率达到10^–5时FLAC 3D自动停止计算。

在计算隧道影响渗流场范围前需生成模型初始渗流场，即隧道未开挖前的渗流特征。根据前期获得的水位点高程设置模型边界孔压，初步计算至稳定状态。

根据施工条件，模型计算共分为2个阶段：开挖后、二次衬砌后。根据对路罗隧道周边岩体进行的钻孔取芯试验，并对岩芯开展了室内三轴渗流试验。结果表明，岩石渗水主要为裂隙透水。结合工程前期的地勘调查资料，最终确定岩体渗流参数，即渗透系数为0.06 m/d。经换算为软件格式的参数后为7.1e–11。模型边界条件：底部为不透水条件，顶部为自由状态。隧道在开挖后模拟条件为透水边界，二次衬砌施加后模拟条件为不透水边界。

为了全面验证隧道开挖对地下渗流的影响，本研究分别对比同一个剖面不同时期的渗流场分布特征，得出隧道开挖在不同时期的影响范围。沿隧道轴向方向，垂直隧道轴线自西向东共取5个剖面（每个剖面间距600 m）。

剖面一渗流场在全断面开挖完成后隧道周围形成“漏斗”形渗流区域，且主要影响隧道上部渗流场，对下部影响深度较浅。隧道两侧180 m范围外无明显影响；对隧道下方90 m范围外无明显影响；隧道上方影响一直到地面。二次衬砌施工完成后，渗流水位得到恢复，下部影响深度较浅。

剖面二渗流场隧道两侧180 m范围外无明显影响；对隧道下方50 m范围外无明显影响；隧道上方影响一直到地面。二次衬砌施工完成后，隧道两侧145 m范围外无明显影响；对隧道下方40 m范围外无明显影响。

剖面三渗流场隧道两侧100 m范围外无明显影响；对隧道下方40 m范围外无影响；隧道上方影响持续至地面。二次衬砌施工完成后，隧道两侧50 m范围外无明显影响；对隧道下方30 m范围外无影响。

剖面四渗流场隧道两侧110m范围外无明显影响；对隧道下方45 m范围外无明显影响；隧道上方影响一直到地面。二次衬砌施工完成后，隧道两侧60 m范围无影响；对隧道下方30 m范围外无影响。

剖面五渗流场隧道两侧150 m范围外无明显影响；对隧道下方50 m范围外无明显影响；隧道上方影响一直到地面。二次衬砌施工完成后，隧道两侧100 m范围外无明显影响；对隧道下方40 m范围外无明显影响。

5 结论

（1）以路罗隧道及周边水域为工程背景，借助无人机倾斜摄影测量技术，通过拾取地形信息，系统的构建了一种复杂地质精细化建模。

（2）汇水分析结果表明研究区三大流域中，邢台大峡谷水域的面积最大，占据隧址区53.36 %的面积，区域内的流量占比仅33.31 %，整体的集水能力最弱，相比周公山流域要弱18.85 %，集水能力仅有前营隧道平导口流域的38.35 %。研究结果表明：隧道修建下游区域，即邢台大峡谷水域的集水能力最弱。

（3）通过构建隧道开挖影响范围内的渗流模型，分析地下水运移关系。根据数值模拟发现，当二次衬砌施工完成后，渗流水位将得到一定程度地恢复，隧道两侧145 m范围外无明显影响；隧道下方40 m范围外无明显影响。由于隧道修建在邢台大峡谷上游，邢台大峡谷景区以及下游均距离隧道超过了90 m的直线距离，因此基于数值模拟认为，隧道的修建对下游的渗流影响几乎可以忽略。